RSA 是 1977 年由三位數學傢 Rivest Shamir 和 Adleman 設計的一種非對稱加密算法,名稱是三人名字的首字母。
RSA 算法非常可靠,密鑰越長就越難破解。
其它加密算法,包括:ECDH、AES,及量子計算時代的 PQC DS、PQC KEM。
據已披露文獻,目前被破解的最長 RSA 密鑰是 232 個十進製位,也就是 768 個二進製位。
可這樣認為,1024 位的 RSA 密鑰基本安全,2048 位的密鑰會更安全 (量子計算機除外)。
由於通過數學算法加密和解密 RSA, 效率會比較低; 因此, RSA 的主戰場一般是加密比較小的數據。
如對大數據先進行對稱加密, 再用 RSA 給對稱加密的 KEY 進行加密 (或加密 Hash 值 ), 也就是數字簽名。
指在一個大於 1 的自然數中, 除 1 和整數本身外, 不能被其他自然數整除的數。
若 N 個整數的最大公因子為 1, 則稱這 N 個整數互素。
模是 Mod 的音譯, 和模運算緊密相關的一個概念就是同餘。 數學上, 當兩個整數除以同一個正整數, 若得相同餘數, 則二整數同餘。
任意給定一個正整數 n, 在小於等於 n 的正整數之中, 有多少個與 n 構成互質關係? 計算這個值的方法就叫做歐拉函數,以 φ(n) 錶示。
和 8 互質的是 1 2 3 4 5 6 7 8。
若 n 是質數的某一個次方, 即 n = p^k (p 為質數,k 為大於等於 1 的整數), 則 φ(n) = φ(p^k) = p^k - p^(k - 1)。
如 φ(8) = φ(2^3) =2^3 - 2^2 = 8 - 4 = 4。
和 7 互質的是 1 2 3 4 5 6 7。
若 n 為質數, 則 φ(n) = n - 1。 因為質數與小於它的每一個數, 都構成互質關係。
如 5 與 1 2 3 4 都構成互質關係。
若 n 可分解成兩個互質的整數之積, 即 n = p * k, 則 φ(n) = φ(p * k) = φ(p1) * φ(p2)。

若兩個正整數 m 和 n 互質, 那麼 m 的 φ(n) 次方減去 1, 可以被 n 整除。
如 8 和 7 互質, 那麼 8 的 φ(7) 次方減去 1, 可以被 8 整除。 即 (8 φ(7) - 1) / 7 = (262144 - 1) / 7 = 37449。

歐拉定理的特殊情況, 若兩個正整數 m 和 n 互質, 且 n 為質數, 那麼 φ(n) 結果就是 n - 1。
如 8 和 7 互質, 且 7 為質數, 那麼 φ(7) = 7 - 1。

若兩個正整數 e 和 x 互質, 那麼一定可以找到某個整數 d, 使得 ed - 1 可被 x 整除 (或者說 ed 被 x 除的餘數是 1), 那麼 d 就是 e 相對於 x 的模反元素。
如 8 和 7 互質, 8 * 5 - 1 可被 7 整除, 那麼 5 就是 8 相對於 7 的模反元素。

根據 歐拉定理 , 由於 1^k ≡ 1, 等號左右兩邊都來個 k 次方。
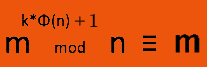
由於 1 * m ≡ m, 等號左右兩邊都乘以 m。

根據模反元素, 因為 e*d 一定是 x 的倍數加 1。
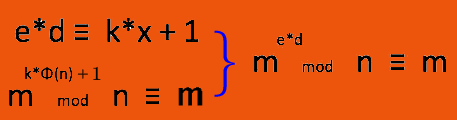
m 的 ed 次方為加密運算, 得到結果 c, c 模以 n 為解密運算, 得到結果 m。
m 通過 n φ(n) e 還有 d 幾個參數, 運算得到的結果,仍然是 m。
注意: 當整數 e 和 φ(n) 互質, 一定有一個整數 d 是 e 相對於 φ(n) 的 模反元素 。
如 m 取值為 4, n 取值為 15 (m 和 n 無需互質,但 m 必須小於 n), 則 φ(n) = 8 (如 1 2 4 7 8 11 13 14)。 若 e 取值為 3, 則 d 可以為 11 19 27 ... (模反元素明顯不止一個,就是解二元一次方程)。
若按這種算法進行加密 解密, 加密的結果會非常大, 明文數據將非常小 (雖然 RSA 用於加密的數據也很小, 但沒這麼大懸殊)。 真正的 RSA 要更加強大, 那麼 RSA 是怎麼演變來的呢? 早期很多數學傢也停留在瞭這一步, 直到 1967 年齣現迪菲赫爾曼密鑰交換打破瞭僵局。
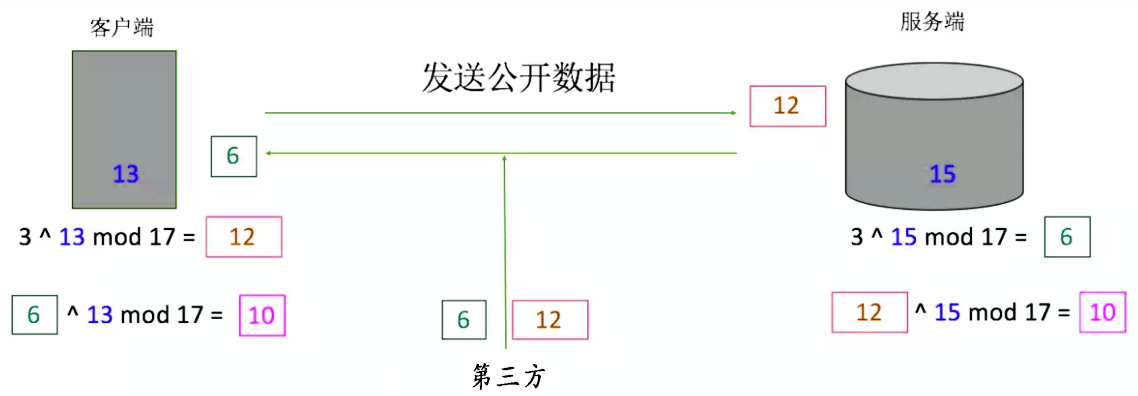
隨機數 15 僅服務器擁有, 3^15 mod 17 = 6, 然後把公布 6 並發送給客戶端。 拿到客戶端的 12, 然後 12^15 mod 17 = 10 (10 就是交換得到的密鑰)。
隨機數 13 僅客戶端擁有, 客戶端用 3^13 mod 17 = 12, 然後公布 12 並發送給服務器。 拿到服務器的 6, 然後 6^13 mod 17 = 10 (10 就是交換得到的密鑰)。
隻能拿到 6 和 12, 因為沒有私鑰 13 15, 所以沒法得到結果 10。
6^13 mod 17 和 12^15 mod 17 的結果都為 10, 這就是迪菲赫爾曼密鑰交換的核心規律。
如 3^3 mod 17 = 10 再 10^2 mod 17 和 3^2 mod 17 = 9 再 9^3 mod 17 的結果都是 15。
m^e % n = c 是加密,c^d % n = m 是解密,m 是原始數據,c 是密文,公鑰是 n 和 e,私鑰是 n 和 d,所以隻有 n 和 e 是公開的。
加密時要知道 φ(n) 的值, 最簡單方式是 2 質數之積, 彆人想破解 RSA 也要知道 φ(n) 值, 就要對 n 進行因數分解。
若不想 m 被破解, n 的值就要非常大, 長度可為 1024 或 2048 位二進製。
Python 3.6.8 (tags/v3.6.8:3c6b436a57, Dec 24 2018, 00:16:47) [MSC v.1916 64 bit (AMD64)] on win32 Type "copyright", "credits" or "license()" for more information. >>> 7 ** 3 % 15 13 # 加密 >>> 13 ** 19 % 15 7 # 解密 >>> 5 ** 23 % 66 59 # 加密 >>> 59 ** 7 % 66 5 # 解密 >>>
以上為通過 數字 IDE Shell 選項卡獲得的結果。
其中, n = 15 (隨機數), 則 φ(n) = 8 (如 1 2 4 7 8 11 13 14), m = 12 (隨機數,必須比 n 小), e = 3 必須與 φ(n) 互質。
d = 19 (也可為 3 11 等),必須與 φ(n) 互質,且 (ed - 1) / φ(n) = 整數。
某些特殊 n e d 值的組閤, 一係列每 m 值 == 每加密 c 值 == 每解密 m 值。 由於每次加密 中間值 解密始終保持不變, 沒有加密 (相當於明文)。
有時 e == d, 也能完美加密解密; e d 值還可大於 n。
另請參閱:
版權聲明: 本文為獨傢原創稿件,版權歸 樂數軟件 ,未經許可不得轉載。